Hình tứ giác là một trong những khái niệm cơ bản trong hình học, mang đến nền tảng cho việc hiểu biết về các hình dạng phức tạp hơn. Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu về hình tứ giác, các loại tứ giác phổ biến, cùng với cách tính chu vi và diện tích của chúng.
1. Hình Tứ Giác Là Gì?
Hình tứ giác, hay còn gọi là đa giác bốn cạnh, có bốn đỉnh và bốn cạnh. Chúng ta có thể hình dung tứ giác như một hình dạng không có bất kỳ hai đoạn thẳng nào cùng nằm trên một đường thẳng. Tùy thuộc vào việc các cạnh và góc của nó như thế nào, tứ giác được chia thành nhiều loại như:
- Hình chữ nhật
- Hình vuông
- Hình thoi
- Hình bình hành
- Hình thang
Mỗi loại tứ giác có những đặc điểm và tính chất riêng, điều này tạo ra sự phong phú cho hình học và ứng dụng trong thực tế.
2. Cách Tính Chu Vi Hình Tứ Giác
2.1. Định Nghĩa Chu Vi
Chu vi của một hình tứ giác là tổng độ dài của tất cả bốn cạnh của nó. Đây là một khái niệm cơ bản nhưng quan trọng đối với bất kỳ ai bắt đầu tìm hiểu về hình học.
2.2. Công Thức Tính Chu Vi
Công thức để tính chu vi của tứ giác được biểu diễn như sau:
C = a + b + c + d
Trong đó:
- C là chu vi của hình tứ giác.
- a, b, c, d là độ dài các cạnh của tứ giác.
2.3. Ví Dụ Tính Chu Vi
Bài 1: Tính chu vi hình tứ giác có độ dài các cạnh là: 5 cm, 7 cm, 3 cm và 4 cm.
Lời Giải:
Chu vi hình tứ giác là:
C = 5 + 7 + 3 + 4 = 19 cm.
Đáp số: 19 cm.
Bài 2: Tính chu vi hình thang có độ dài các cạnh là: 10 m, 6 m, 12 m, và 8 m.
Lời Giải:
C = 10 + 6 + 12 + 8 = 36 m.
Đáp số: 36 m.
3. Diện Tích Hình Tứ Giác
3.1. Định Nghĩa Diện Tích
Diện tích của một hình tứ giác là số đo không gian bên trong nó. Tuỳ thuộc vào loại hình tứ giác mà chúng ta sẽ có những công thức khác nhau để tính diện tích.
3.2. Các Công Thức Tính Diện Tích
3.2.1. Diện Tích Tứ Giác Thường
Công thức tính diện tích tứ giác bất kỳ là:
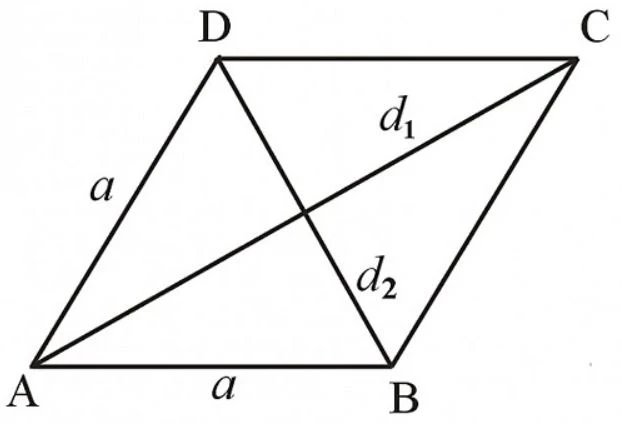
S = ½ (d1 d2 * sin A)
Trong đó,
d1 và
d2 là độ dài hai đường chéo và
A là góc giữa hai đường chéo.
3.2.2. Diện Tích Hình Thang
Đối với hình thang, công thức tính diện tích là:
S = ½ h (a + b)
Trong đó:
- a và b là độ dài hai cạnh đáy.
- h là chiều cao.
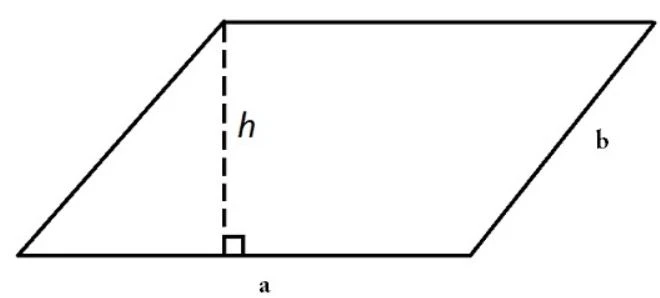
3.2.3. Diện Tích Hình Bình Hành
Diện tích hình bình hành được tính bằng:
S = a * h
Trong đó:
- a là độ dài một cạnh.
- h là chiều cao từ cạnh đó.
3.2.4. Diện Tích Hình Thoi
Công thức tính diện tích hình thoi là:
S = ½ d1 d2
Trong đó:
- d1 và d2 là độ dài hai đường chéo.
3.2.5. Diện Tích Hình Chữ Nhật
Diện tích của hình chữ nhật được tính bằng:
S = a * b
Trong đó:
- a là chiều dài.
- b là chiều rộng.
3.2.6. Diện Tích Hình Vuông
S = a²
Trong đó
a là độ dài cạnh hình vuông.
3.3. Ví Dụ Tính Diện Tích
Bài 1: Tính diện tích hình thang có các cạnh đáy lần lượt là 10 m và 6 m, chiều cao 4 m.
Lời Giải:
S = ½
4 (10 + 6) = ½
4 16 = 32 m².
Đáp số: 32 m².
Bài 2: Tính diện tích hình bình hành có cạnh đáy 8 cm và chiều cao 5 cm.
Lời Giải:
S = 8 * 5 = 40 cm².
Đáp số: 40 cm².
4. Bài Tập Thực Hành
Để củng cố kiến thức, hãy thử sức với các bài tập dưới đây.
Bài 1: Tính chu vi hình tứ giác có độ dài các cạnh là: 4 cm, 7 cm, 3 cm và 5 cm.
Bài 2: Một hình thang có hai đáy lần lượt là 12 m và 8 m, chiều cao là 6 m. Tính diện tích của hình thang đó.
Bài 3: Tính diện tích hình tứ giác MBND, biết rằng hình chữ nhật ABCD có chiều dài 24 cm và chiều rộng 16 cm.
5. Kết Luận
Hình tứ giác là một phần quan trọng trong hình học, không chỉ giúp chúng ta hiểu về các hình dạng đơn giản mà còn mở ra một cánh cửa đến với những kiến thức phức tạp hơn. Việc nắm rõ các công thức tính chu vi và diện tích của các hình tứ giác sẽ là nền tảng vững chắc cho việc giải quyết các bài toán hình học sau này.
Hy vọng bài viết này sẽ cung cấp cho bạn những kiến thức bổ ích và thú vị về hình tứ giác, cùng với cách tính chu vi hình tứ giác một cách rõ ràng và dễ hiểu. Chúc bạn học tốt và thành công trong việc áp dụng những kiến thức này vào thực tế!





